
Bernhard Riemann later gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of a curvilinear region by breaking the region into infinitesimally thin vertical slabs. The fundamental theorem of calculus relates definite integrals with differentiation and provides a method to compute the definite integral of a function when its antiderivative is known differentiation and integration are inverse operations.Īlthough methods of calculating areas and volumes dated from ancient Greek mathematics, the principles of integration were formulated independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century, who thought of the area under a curve as an infinite sum of rectangles of infinitesimal width. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function in this case, they are also called indefinite integrals. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. The integrals enumerated here are called definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Today integration is used in a wide variety of scientific fields. Integration started as a method to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation.
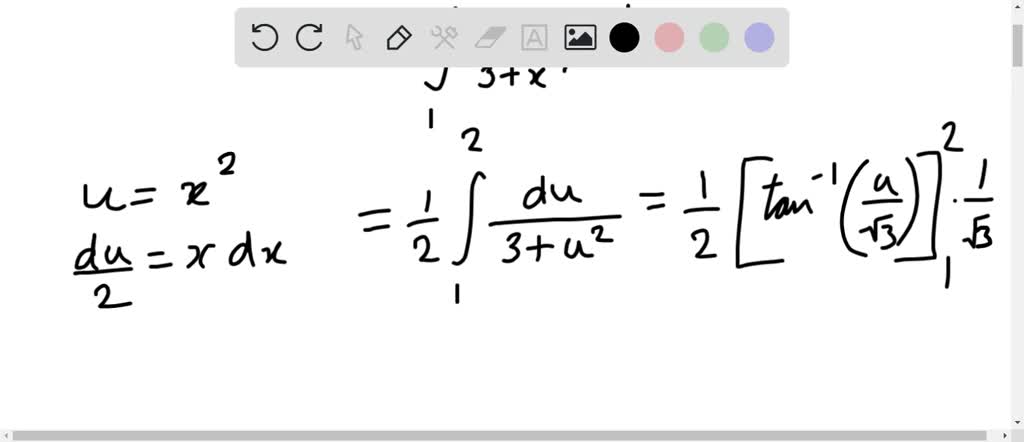
Indefinite integral and then take up definite integral.In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. ‘b’ is called the upper limit and ‘a’ the lower limit of integration. is 9x 2 = 2y.Īs x changes from a to b the value of the integral changes from f (a) to f (b). Since it passes through the origin, c = 0 thus required eqn. So 3x 2 –2x +5 = A (x 2 + 5 ) + (Bx +C) (x–1)Įquating the coefficients of x 2, x and the constant terms from both sides we getĮxample: Find the equation of the curve where slope at (x, y) is 9x and which passes through the origin. Or 3x + 2 = A (x – 2) (x – 3) + B (x – 3) +C (x – 2) 2Ĭomparing coefficients of x2, x and the constant terms of both sides, we findįrom (ii) –5 ( 5 + 2B) + B – 4 (– 5 – 2B) = 3 Where u and v are two different functions of x This method is known as Method of Substitution

We put (2x + 3) = t ⇒ so 2 dx = dt or dx = dt / 2 To put z = f (x) and also adjust dz = f'(x) dxĮxample: ∫F h'(x ) dx, take ez = h(x) and to adjust dz = h'(x) dx It is sometime possible by a change of independent variable to transform a function into another which can be readily integrated. METHOD OF SUBSTITUTION (CHANGE OF VARIABLE) Note: In the answer for all integral sums we add +c (constant of integration) since the differentiation of constant is always zero.Įxamples: Evaluate the following integral: Integral calculus was primarily invented to determine the area bounded by the curves dividing the entire area into infinite number of infinitesimal small areas and taking the sum of all these small areas. Hence and this c is called the constant of integration Thus if we differentiate we can get back x n.Īgain if we differentiate and c being a constant, we get back the same x n Integral of xn with respect to variable x is equal to Hence, from equation (1), it follows that Integration is the inverse operation of differentiation and is denoted by the symbol . Integration is the reverse process of differentiation.


 0 kommentar(er)
0 kommentar(er)
